Tibetan editionSanskrit edition Click here for pdf of Sankrit edition Abhayākaragupta was one of the most important of the Indian masters of the Kālacakra cycle, and abbot of Vikramaśīla monastery, probably in the late 11th or very early 12th century CE – within a century after the Kālacakra Tantra was translated into Tibetan. Elsewhere on this site is his description for creating the Kālacakra maṇḍala; the present pages deal with his work on Kālacakra astronomy and the calendar, the Kālacakrāvatāra (dus kyi 'khor lo la 'jug pa, "Introduction to Kālacakra"). Several years ago, I obtained from The Asiatic Society in Calcutta, India, a copy of the sole known surviving Sanskrit manuscript of this text. As this was written in medieval Bengali script, I was barely able to read a single word of the text. However, this was recently transcribed into Devanāgarī for me by an expert in medieval Bengali, Vijayarāja Vajrācārya, working at the Central University of Tibetan Studies in Sarnath, India. The main purpose of these pages is to make this easily readable Sanskrit edition of the text freely available; but, this is also accompanied by an edited edition of the Tibetan translation of the Kālacakrāvatāra and an English description of the text's contents. (As yet, it has not been translated into English.) The text explains the method for creating and correcting a calendar as given in the Kālacakra Tantra and its commentary, the Vimalaprabhā. It quotes these texts often, following their structure, and explains the creation of the calendar in more straightforward terms. The translation is, however, relatively old, compared to the much revised Kālacakra Tantra and commentary. The quotes from the tantra and commentary are therefore usually similar to, but not exactly the same as, the equivalent sections in those later texts. One quote is worth mentioning by way of example. The Siddhānta section of the Vimalaprabhā quotes a set of verses said to be from the Kālacakra Mūlatantra. Two lines of this section are quoted in the Kālacakrāvatāra; these describe the need to adjust the Sun's longitude. The Sanskrit is the same in The Asiatic Society's Kālacakrāvatāra as in the CIHTS edition (Sarnath) of the Vimalaprabhā: aśuddhe sūryabhoge'smin śodhitā maṅgalādayaḥ / {19}My translation of this in English is: "If the longitude of the Sun is wrong, just like the branches of a tree with a rotten trunk, Mars and so forth which are subtracted from it will not be correct."Now, the Tibetan, first from the Derge edition of the Kālacakrāvatāra: nyi ma'i longs spyod ma dag 'dis //And now from the Derge edition of the Vimalaprabhā: nyi ma'i longs spyod ma dag na //They are quite different, although the basic sense is the same. However, the Vimalaprabhā does properly bring out the fact that the slow motion longitudes of the planets are subtracted (śodhitā) from that of the Sun; this a point that is made elsewhere, because as the true fast motion longitudes of the planets depend on that of the Sun, then if the longitude of the Sun is wrong, so will be the true longitudes of the planets. That is not clear from the earlier translation.
For the Tibetan edition available here, three different editions have been compared: Derge, Narthang and Cone. I have not preserved all the variations between the texts – this is not a critically edited edition – but have tried to create the best possible reading to provide a usable edition. The Sanskrit has been invaluable in choosing between differences between these different editions, but it also seems that there would be differences between the present Sanskrit edition and the original that was translated into Tibetan, if that should ever come to light. Brief outline of the KālacakrāvatāraAs mentioned above, the text explains the section in the Vimalaprabhā on the Kālacakra calendar. Much of this consists of the calculations for the calendar. A worked example of these calculations is given here. In the following, numbers in square brackets identify the relevant sections in the Tibetan text.The text starts [1] by calculating the number of years since the epoch. The Tantra takes as an intermediate epoch 1027 CE, counts back 403 years and then forward 182, to reach the epoch 806 CE. The Kālacakrāvatāra takes an intermediare epoch of 1087 CE and counts back 463 years. The point is to find for the year for which a calendar is to be created, the years since the 806 epoch. The text then goes through the calculations for the [2] true month, the [3] mean weekday, [4] lunar anomaly and [5] solar longitude. Next, [6] the stepping functions and their interpolation methods are described for the weekday and solar longitude to convert from mean to true values. Once the true values have been calculated, the text then describes [7] how to determine the longitude of the Moon, followed by the yoga and karaṇa. The names of the various components are then listed: [8] the weekdays, lunar dates, lunar mansions, yogas and karaṇas – these being the five componants (yan lag lnga) of the calendar. Next [9] comes the association of the lunar mansions with the zodiacal signs, the planetary rulerships of the 12 signs and the calculation for the change of year. At the end of this section, in the Sankrit text 12 sets of three numerals are listed. These are not given in the Tibetan translation, but they are given in symbolic form in the verse above: "zla ba ri dang 'byung ba..." The way in which the numerals are formatted, is however, rather odd. The verse is actually the last three lines of verse 37 of the first chapter of the Kālacakra Tantra plus the first line of verse 38. In English, with the numerals given in brackets after their symbolic representations, this is: Moon (1) mountain (7) element (5) knowledge (4) with quality (3) arrow (5) 'having a hare' (1), and mountain (7) Moon (1), for the third.The Vimalaprabhā explains these numbers as being weekdays and nāḍī – the first three representing 1;57, the next three 4;53, and so on. These are values needed for calculating the time at which the Sun enters the various zodiacal signs, starting with Aries. As I have written elsewhere, "These numbers are not consistent, and have clearly not been derived from the theory (siddhānta). Rather, they must be based either on observation or some other source."
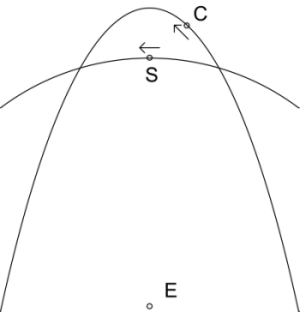
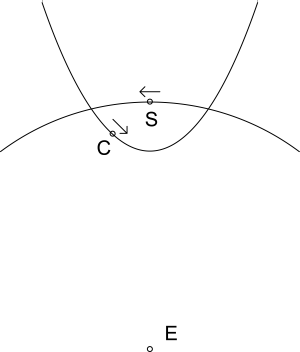
Next [12] comes the calculation for the longitudes of the head and tail of Rāhu, the Moon's ascending and descending nodes. This section includes a description of the determination of both solar and lunar eclipses and some discussion of the characteristics of eclipses. The final calculation [13] is for a comet, Ketu. This presumably was derived from observations of a real comet many centuries ago, but this has never been satisfactorilty identified. There is no good reason for identifying this with Comet Encke, as has been suggested by Dieter Schuh. The period of comet Encke is given by NASA as just over 1,200 days (3.3 years). The period of Ketu is given as 75 lunar months – 6.06 years. (Even if, as does Schuh, you interpret the early writings as suggesting that Ketu's period is half this figure, it is still significantly different from Encke. In his article, Schuh refers to the writer Khyenrab Norbu, who unambiguously gives the period as 75 lunar months.) Now the orbit of a short period comet such as Encke will be subject to planetary perturbations and non-gravitational effects (due to expelling material when near the Sun), and it is remotely possible that Ketu's orbit was disturbed and became the orbit we see today as Encke's. But given that the NASA link shows only one comet with a period of less than four years, and 12 comets with periods of between five and seven years, it is far more likely that if we can still see Ketu that is has become one of this group, rather than Encke. Also, changes have been observed in the period of Encke (the first comet for which this was observed): the period has been getting shorter, and not longer, as would be required for it to have been Ketu with a period of 3.03 years. The writings on Ketu are far from satisfactory, and are more an attempt to explain the motion of a comet in terms of the four motions that are known from planetary theory – see the next paragraph. However, the numbers do not quite fit this theory, which is illustrated in the diagrams on the right (the period would have to be close to an integral multiple of six months). The theory states that at the beginning of a cycle, as the comet enters its fast motion quadrant, it is first visible to the naked eye like a star, and then develops a tail. It is seen "in front of the Sun", ie. rising shortly before the Sun (when the Earth is on the other side of the Sun from the comet's perihelion). It then disappears behind the Sun, not to be seen again until retrograde, 75 months later, at the end of the slow quadrant. At that time it is "behind the Sun", setting just after the Sun (when the comet's perihelion is on the same side of the Sun as the Earth). No doubt this theory is based on observations of at least one or more comets, and the intriguing thought remains that perhaps the Kālacakra astronomers did predict one or more reappearances of a comet – several hundred years before Halley! The text then describes [14] the four motions of the planets. When the "fast" (geocentric) longitudes of the planets are calculated, the "slow" (heliocentic) longitude of the planet is subtracted from that of the Sun. Taking Mars as an example, at the time of conjunction, when the planet is directly behind the Sun from the Earth's point of view, the difference between the slow longitude of Mars and that of the Sun is zero. This is the start of the cycle of the four motions of the planet. At conjunction, Mars is travelling at its fastest angular velocity relative to the Earth. A little later, Mars becomes visible again as it is no longer masked by the light of the Sun, and is seen in the morning shortly before sunrise. As the weeks pass, the fast longitude moves further ahead of the slow longitude, but Mars also gradually slows down. The period between conjunction and when the difference between the slow longitude and the Sun is somewhat over 90° is called the fast motion (śīghracāra, myur bar rgyu ba). Strictly speaking, the term should apply to conjunction, the beginning of the quadrant. Mars rapidly slows down during the second quadrant until shortly before the Sun-slow difference is half a circle when it goes retrograde, appearing to move backwards in the sky. This second quadrant is called the slow motion (mandacāra, bul bar rgyu ba). As the third quadrant starts, the retrograde motion slows, and soon the planet starts to move forward again. Because it starts with the planet in retrograde motion, this third quadrant is called the reversing motion (vakracāra, yon por rgyu ba). The planet gradually picks up speed through the third and fourth quadrants, the fourth being called the advancing motion (nirgamacāra, 'thon por rgyu ba). At the end of the fourth quadrant, Mars is last seen setting just after the Sun in the evening, shortly after which the cycle is complete and Mars is again in conjunction with the Sun. In later writings, the last three motions are usually translated into Tibetan as dal ba, 'khyogs po and 'byung ba, respectively. The first two quadrants, the first half-circle, are called progressive (krama, rim pa), because the fast longitude is greater than (ahead of) the slow, and the last two quadrants are called regressive (utkrama, rim min), because the fast longitude is less than (behind) the slow. In each of the first quadrants of each half-circle, the difference between the fast longitude and the slow is increasing, and in the second quadrants of each half-circle that difference is decreasing. In the first quadrant the planet is said to be facing east, in the second south, in the third west, and in the fourth north. In practical terms, these quadrants determine the difference that needs to be applied to the slow longitude to yield the fast longitude, and whether this difference is added or subtracted. They are therefore very important to the theory of the calculations. Next, the text describes [15] the increase and decrease in the length of day and night in several different countries, starting with India. It describes how, as the passage of the Sun moves from being over the southern perimeter of fire, travelling north until it is over the edge of the great snowy mountains, the length of day increases by one tenth, and the length of night decreases by the same amount. With 60 nāḍī (dbyug gu) in each day and 60 liptā (chu srang) in each nāḍī this works out to a total change of six nāḍī, or a change each day of close to two liptā – 48 seconds. This would make the latest sunrise, at winter solstice, to be at about 6.36am. This would be correct for central India, although the rate of change is certainly not constant as is suggested in this text. The text then gives the total change for several other regions: Tibet, one ninth; Khotan, one eighth; China and Sambhala, one seventh (the Vimalapabhā gives Sambhala as one sixth); the region of Kailash, one sixth; and, in the region north of Kailash, to the snowy mountains, the change each day in day and night is three liptā and four breaths. Next [16], are the characteristics of the circle of the lunar mansions and zodiac signs. Everything that has gone before is then described as being the karaṇa-path (karaṇamārga, byed pa'i lam). However, [17] it states that in this system, the longitude of the Sun does not remain accurate and therefore a method has to be applied to correct the solar longitude. This involves setting up a gnomon to determine the time of the winter solstice and then adjust the longitude of the Sun accordingly. The text first quotes the verse mentioned above about how the longitudes of the planets will be wrong if that of the Sun is wrong. It states that therefore the siddhānta method will be taught: on level ground, in the middle of a circle one cubit (hasta, khru) in size, place a gnomon (chāyā, shing gi grib ma) that is one span (vitasti, mtho gang ba) in height. (These are presumably minimum sizes – the larger the equipment, the easier it is to make accurate measurements.)
Take a cord and fix it on one of the marks; using the cord, describe a large arc reaching to the other mark. Then, from the second mark, repeat the process to form two intersecting arcs making the form of a fish. Of the two intersecting points, one indicates north and the other south. Having identified these two directions (and presumably drawn appropriate lines to indicate them), the two arcs can be erased. Then, from approximately ten days before the winter solstice is expected, each day, around noon, inspect the shadow. Identify the day when the midday shadow – exactly along the north-south line – stops increasing in length towards the north and starts to decrease in length. That is the day when the Sun changes to its northward passage. For that day, set the primary definition, the longitude of the Sun, to 0° Capricorn, ie. 20;15 in lunar mansions and nāḍī. Adjust following days accordingly, adding 0;4,26 to the mean solar longitude each day and then apply the previously explained interpolation methods to determine the true solar longitude for each day. This method assumes that at 0° Capricorn, the winter solstice, and at 0° Cancer, the summer solstice, the correction to be applied to the mean solar longitude is zero, as the mean and true solar longitudes are identical. Abhayākaragupta then [18] finishes his text with a comment that the results of the weekdays, lunar dates, lunar mansions, and so forth – ie. astrology – are easily understood elsewhere, and therefore these things are not explained in his text.
|